|
|
Semiconductor Junctions:
p-P and n-N Heterojunctions
nP and pN that we have covered in the previous section are called anisotype heterojunctions. Where the doping in the two semiconductor materials, as in nN and pP, they are called isotype heterojunctions. The energy band diagrams for isotype heterojunctions utilise the same expressions as were derived for the anisotype cases . Again, the energy band diagram is based on ΔE c and ΔE v , together with the requirement that the Fermi level is constant at thermal equilibrium. To model the situation exactly requires a bit more theory. In this isotype heterojunction model, we simply modify the equations derived previously and reconsider the built in voltage for the isotype heterojunctions. In general, we will derive the voltage drop at x = 0 also shown a way to model these isotype heterojunctions.
When p-type and P-type semiconductors are contacted, a space charge region is created. The charge distribution is
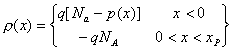
(1)
Note that far away from the junction
The electric field satisfies
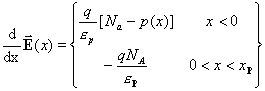
(2)
Since electric field is zero at minus infinity and x = x p . Equation (2) can be integrated from minus infinity to 0 - to obtain
(3)
where
(4)
The boundary condition gives
(5)
and
(6)
or
(7)
The electric field profile will be
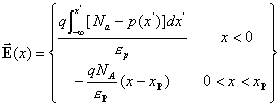
(8)
This electric field profile is very similar to nP heterojunction in figure 8. Using the Boltzmann distribution
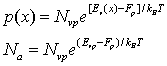
(9)
where
Using the relationship between electrostatic potential and electric field, we got the relationship between valence energy band edge and electric field, that is ,
(10)
where
(11)
and
(12)
Using the above equations, we obtain a differential equation for E v (x) from equation (8)
(13)
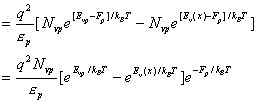
Using relation (12)
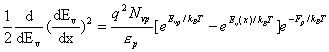
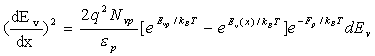
(14)
Integrating from x= minus infinity to 0 -
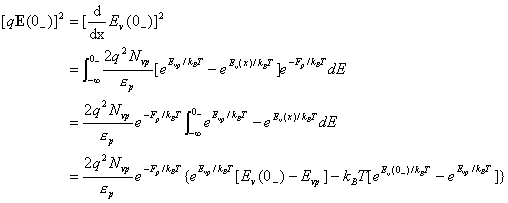
(15)
with
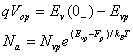equation (14) becomes
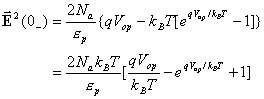
(16)
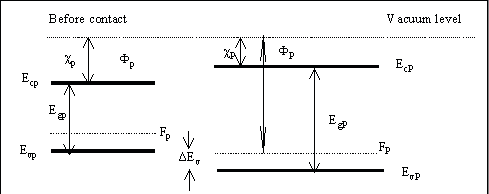
Figure 1. Bandedge profile of heterojunction before contact. |
If we look at the energy band diagram before contact as shown in figure 1. The built voltage will be
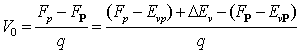
(17)
The difference has been taken as F p -F P , so that forward bias is for the positive potential connected to the P-side. In this case, V 0 will be
positive if
negative if
(18)
or even
For positive or zero built in voltage, it will generally be near zero, the energy band diagram is then given by expressions similar to the nP case, simply replacing all the donor concentration, which is N d , to acceptor concentration that is N a . However, if built in voltage were too negative, the energy band diagram is given by expressions similar to that of pN heterojunction case with N D replaced by N A .
From equation (17), we and obtain an expression for P side, which is
at P side.
(19)
we obtain at x= 0
(20)
(21)
Therefore
(22)
Thus from equations (16) and (17)
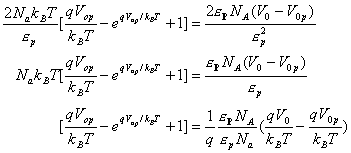
(23)
,
and
, and hence
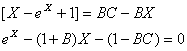
(24)
The solution using Matlab is given by
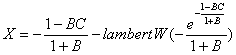
(25)
where LambertW( x ) is the solution to w *exp( w ) = x and LambertW( x ) is linear when x <<1. B is usually very large, so that we can ignore the lambertW and hence
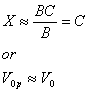
(26)
Semiconductor n-N Heterojunction
For nN heterojunction the built in Voltage will be
(27)
ΔE c is generally larger than the difference (E cn - F n ) (E cN F N ), the built in voltage will be positive. The expressions for the energy band diagrams are similar to the p-N heterojunction case with Na replaced by N d.
The energy diagram before contact is shown at figure 2
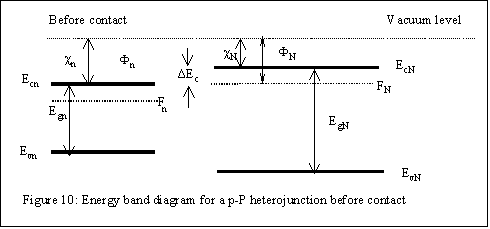
Figure 2. Bandedge profile before contact in p-P heterojunction. |
Following the similar steps as for the p-P heterojunction, we can find an equation at x =0 for electric fields at both sides. The displacement vector must continuous at zero, therefore we obtain:
(27)
the only unknown V on is obtained by solving equation (27)
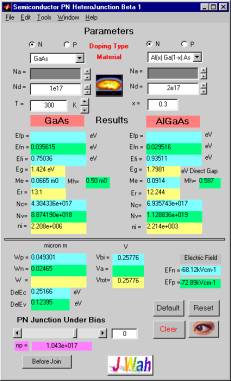
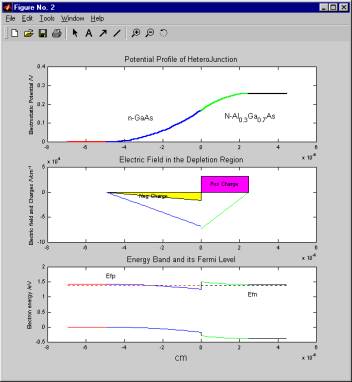
n-N Heterojunction and p-P Heterojunction Modelling
|
|
|
|