Calculating the Fermi Level
Let us define dimensionless units ηF and r
(1)
where EF is the Fermi energy and Ec is the energy of the bottom of the conduction band. In the reduced carrier density r, N is the carrier density and NC is the effective density of states in the conduction band. Using our dimensionless units, the Fermi integral is defined by
(2)
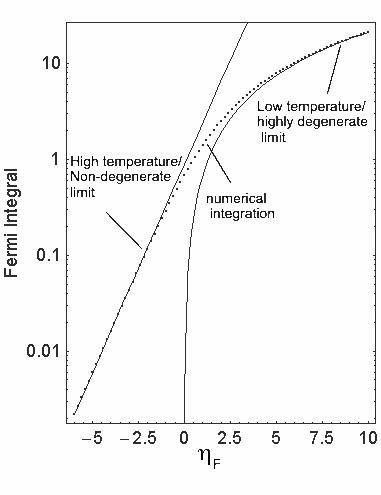
Figure 1. Numerical integration of the Fermi integral (dotted line) and limiting approximation functions (solid lines).
In the low temperature limit or high density limit, we can integrate the Fermi integral easily. Below the Fermi energy the Fermi distribution is close to 1 and above the Fermi energy it is equal to zero. Using this information we arrive at the low temperature limit. Thus is a simple matter to integrate giving the result
(3)
The other important limiting case occurs for high temperatures or low carrier densities. In this instance, the Fermi energy is negative relative to the bottom of the conduction band. The Fermi integral becomes:
(4)
The Fermi integral is shown in Figure 1 along with the limiting functions to show how well they approximate the Fermi integral.
An approximation to the Fermi integral that works well with an accuracy of about 0.5 % is the Aymerich-Humet approximation2
(5)
where
(6)
|  These methods are often based on a suitable curve fit to the Fermi integral so there is no physical insight in these approximations 
|
In between the two extremes of low temperature/high densities and high temperature/low density cases, it is useful to have a expression to obtain the Fermi-level. Unfortunately,because the Fermi integral is non-invertable, there is no analytical method to do this. However, many approximations have been developed to enable the Fermi level to be calculated using numerical approximations. These methods are often based on a suitable curve fit to the Fermi integral so there is no physical insight in these approximations. In the following section, numerous approximations are detailed.
Boltzmann Approximation
(7)
Joyce-Dixon Approximation
(8)
The Joyce-Dixon3 approximation is valid for all negative values of ηF as it asymptotes to the low temperature/low density limit but is only valid for positive values of ηF below about 5.
Padé Approximation
(9)
The error in this approximation depends on the value of k1 and k2.
|
k1 |
Error |
valid for hF |
|
4.7 |
0.0004 hF |
hF <9.8 |
|
4.9 |
0.02 hF |
hF <18.8 |
|
5.2 |
0.1 hF |
hF <28 |
(10)
Inverse First-Order Unger Approximation
(11)
where a2 = 0.14645 is valid for h < 2.8 and a2 = 0.15 is valid for ηF < 7.4.
Inverse First-Order Sommerfeld Approximation
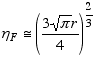if ηF
>20
(12)
Nilsson's Approximation
This method4 works over the entire range of values of ηF with an error of less 1%.
(13)
References
1. L. Coldren, Photonic Integrated Circuits
2. X. Aymerich-Humet, F. Serra-Mestres and J. Millan, Solid State Electronics, 24, pp 981, (1981).
3. W. B. Joyce and R. W. Dixon,Appl. Phys.Lett., 31, pp. 354, (1977)
4. N. G. Nilsson, Phys. Sta. Solidi (a), 19, K75, (1973).