|
|
|
|
Radiative Transitions
There are three radiative transitions that are important in semiconductor lasers that occur between the conduction and valence bands of the material. A schematic diagram of these transitions is shown below:
Figure 1. Radiative recombination processes: a) absoprtion, b) spontaneous emission, c) stimulated emission.
In Figure 1. a) absorption, an electron in the valence band gains energy by absorbing a photon, exciting it to a higher energy level within the conduction band. The energy gained by the electron is equal to the energy of the photon.
![]()
(1)
Not all the electrons interact with the photons of light. The rate that electrons will be absorbed is determined by the number of unoccupied states in the conduction band, the number of occupied states in the valence band and density of photons of energy equal to the transition energy. If p 2 and p 1 are the occupation probabilities of the upper and lower states respectively.
![]()
(2)
A second radiative process, spontaneous emission is shown Figure 1. b). An electron starts out in an excited state in the conduction band. When the electron falls back into the valence band it releases its excess energy in the form of a photon with an energy given by (1). The photon emitted by the electron decaying to a lower energy has a random phase and direction. The rate at which excited electrons will spontaneously emit photons is given by (3) , where A 21 is the transition probability of an excited particle falling into a vacant lower state.
![]()
(3)
At first, that would seem to account for all the radiative transitions, however, there is a third process that can take place. If a photon is strongly coupled with the electron, it can cause it to decay to a lower energy level, releasing a photon of the same energy. The emitted photon has the same direction and phase as the incident photon. It is this process that is responsible for stimulated emission. The rate of stimulated emission, depends on the occupation probabilities of the upper and lower states as before but also on the photon density r(w ) at the wavelength incident photon energy.
![]()
(4)
Comparing (4) and (2) we can see that the stimulated emission process is the reverse of the absorption process. In equilibrium, the rate at which electrons are excited into the conduction band is equal to the rate of electrons falling back to the valence band. Therefore,
![]()
(5a)
or
![]()
(5b)
Solving this equation for
![]() , we find:
, we find:
![]()
(6)
This reduces to:
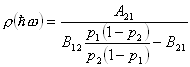
(7)
The term,
![]() is the relative occupation probability between the two energy levels and as we are considering a system in thermal equilibrium, this can be replaced by the Boltzmann equation. (7) becomes,
is the relative occupation probability between the two energy levels and as we are considering a system in thermal equilibrium, this can be replaced by the Boltzmann equation. (7) becomes,
![]()
(8)
![]() In addition, we know the distribution of radiation for a body in thermal equilibrium. It is simply the Planck distribution function.
In addition, we know the distribution of radiation for a body in thermal equilibrium. It is simply the Planck distribution function.
![]()
(9)
Equating (8) and (9) we obtain two important results:
![]()
(10a)
![]()
(10b)
This result was first obtained by Einstein in 1917, so A and B are called the Einstein coefficients . It does not give the values of the coefficient. However, it is possible to calculate the value for A21 from which, the other Einstein coefficients may also be calculated. Further insight can be obtained be studying the ratio of spontaneous emission to stimulated emission. From (8) and (10a) a similar argument leads to an application of the Boltzmann equation and the ratio of spontaneous emission to stimulated emission leads to
![]()
(11)
From this equation it is apparent stimulated emission is dominant when
![]() .
.
The important part of this equation is that the probability of finding an electron in the conduction band has to be greater than the probability of finding an electron in the valence band or alternatively, there must be a population inversion .

|
|