The Hall Effect

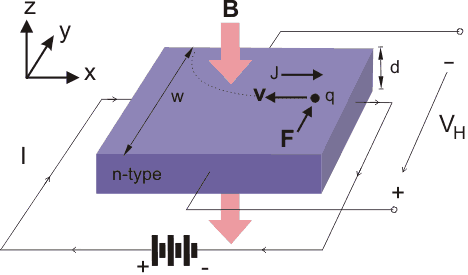
Figure 1. Schematic diagram of the Hall effect. An n-type semiconductor with a current applied across and magnetic field perpendicular to the current exhibits a potential difference perpendicular to both the current and the magnetic field, which is known as the Hall effect.

The force acting on the moving charge carriers in a magnetic field is the Lorentz force.

(1)

F, v and B form a right-handed Cartesian co-ordinate system. Since we have arranged v and B to be perpendicular to each other, the resultant force is also perpendicular to both v and B as shown in (2).

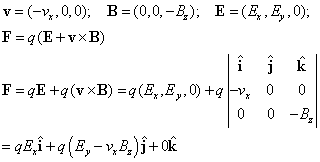
(2)

The force in (2) is reduced to two simple equations which describe the motion of the carriers.

(3 a)

(3 b)

The movement of charge carriers sets up an electric field E_y in the opposite direction to the Lorentz force and this field continues to grow as the charge carriers move to one side of the semiconductor until it balances the Lorentz force. In this situation we have

(4)

The electric field can be calculated from the Hall voltage, V_H, since for a constant electric field,

(5)

where w is the width of the sample.

Since the velocity can be expressed in terms of the current density, E_y can be written as

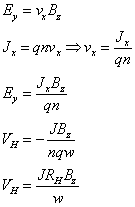
(6)

Where R_H is the Hall constant which is negative if the majority carriers are electrons and positive if the majority carriers are holes. It must be pointed out that, the velocity of the carriers is the result of a statistical measurement and non-linear effects of the magnetic field can alters the results obtained experimentally. Therefore a correction term r_H, the Hall coefficient factor is included in the Hall constant, which can usually take a value between 1 and 1.5.

(7)

If the sample contains both electrons and holes, then the Hall constant is given by

(8)

Since we measure V_H and set the values or measure the values of B_z, I, A and w, we can calculate the n, the carrier density. In addition to being able to measure the charge of the majority carriers the Hall effect can be used to measure the Hall mobility. With a measurement of the Hall coefficient the mobility can be found.

(9)

Where r is the resistivity of the sample which is most commonly obtained using the Van der Pauw technique.

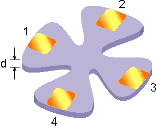
Van der Pauw Technique

The Van der Pauw technique can be used to measure resistivity of a thin, arbitrary-shaped, simply connected, (i.e. one without holes or non-conducting islands) sample with four Ohmic contacts placed on the periphery. The objective of the Van der Pauw technique is to measure the sheet resistance R_s of the sample. Van der Pauw demonstrated that there are two characteristics resistances, R_A and R_B, associated with the four terminals.

Where V₄₃ is the voltage measured across terminals 4 and 3, V₁₄ is the voltage measured across terminals 1 and 4. I₁₂ is the current measure across terminals 1 and 2. I₂₃ is the current measured across terminals 2 and 3. R_A and R_B relate to the sheet resistance through the Van der Pauw equation.

(11)

which can be solved numerically for R_s. The resistivity can then be calculated using

(12)

To obtain the two characteristic resistances, one applies a dc current I into contact 1 and out of contact 2 and measures the voltage V₄₃ from contact 4 to contact 3. Next, one applies the current I into contact 2 and out of contact 3 while measuring the voltage V₁₄ from contact 1 to contact 4. R_A and R_B are calculated by means of the following expressions

(13)

The objective in the Hall measurement in the Van-der Pauw technique is to determine the sheet carrier density n_s by measuring the Hall voltage V_H. The Hall voltage measurement consists of a series of voltage measurements with a constant current and a constant magnetic field B applied perpendicular to the plane of the sample. The sheet carrier density n_s can be calculated via

(11)

To ensure the quality of the result obtained from the Hall measurement several factors must be considered. Primary concerns are Ohmic contacts quality and size, sample uniformity and accurate thickness determination and thermomagnetic effects due to nonuniform temperature and photoconductive and photovoltaic effects which can be minimised by measuring in a dark environment. Also the lateral dimensions must be large compared to the size of the contacts and the sample thickness. Finally, one must accurately measure sample temperature, magnetic field intensity, electric current and voltage.

References

[1] R. P. Feynman, Feynman Lectures on Physics, 3 , ch. 14, (19