Finite Barrier Quantum-Well

In the last section, we looked at the p-n junction. More efficient recombination of electron-hole pairs can be acheived by incorporation of a thin layer of semiconductor material, either p or n type semiconductor with a smaller energy gap than the cladding layers, to form a double heterostructure. (More on this in the future). As the active layer thickness in a double heterostructure becomes close to the De-Broglie wavelength (about 10nm for semiconductor laser devices) quantum effects become apparent. Quatum wells are important in semiconductor lasers because they allow some degree of freedom in the design of the emitted wavelength through adjustment of the energy levels within the well by careful consideration of the well width. A simple model of the energy levels in a quantum well is considered below.
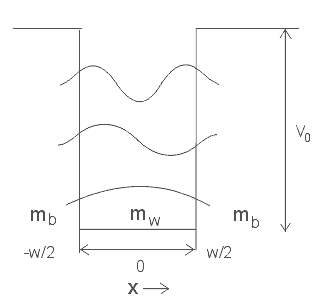
Solving the Schrödinger equation for a finite potential will produce values of the energy levels within the well. Consider a potential well centered on the origin of width w and barrier height V ₀ . Inside the well the potential is zero, the Schrödinger equation.

|x| <w/2 with

(1)

|x| > w/2 with

(2)

For even wavefunctions, the solution of the Schrödinger equation within the well is:

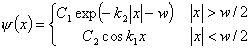
(3)

The wavefunction and its derivative must be continuous at the boundaries of the well.

(4)

(5)

Eliminating C ₁ and C ₂ , we obtain the quantisation condition:

(7)

Similarly for odd wavefunctions,

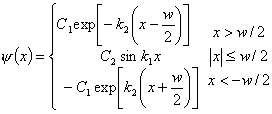
(8)

The boundary conditions give

(9)

The eigenequation is thus

(10)

The solutions for the quantised eigenenergies can be obtained by k ₁ w and k ₂ w using a graphical approach since

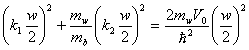
(11)

and

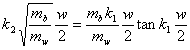for even solutions

(12)

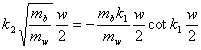for odd solutions

(13)

In the case where the mass of the particle in the barrier differs from the mass of the particle in the well, then we introduce a scaling factor to account for this.

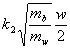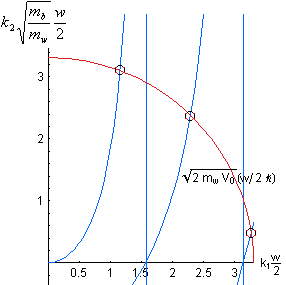
plotting against produces the graphs below, the potential generates a circle of radius . The energy levels in the well are found from the intersection of the tangent and cotangent relationships with the circle within the positive quarter.

Figure 1. The graphical solution for finite barrier quantum well and energy levels derived from graphical solution.

Wah, has written a Matlab program to solve this equation using this method. Click here . Alternatively, use the Mathematica version written by me.

Back to the semiconductors