Diffusion

Diffusion is the movement of particles from regions of high concentration to regions of low concentration. To illustrate diffusion in a semiconductor, we consider the rather simplistic case in which a concentration gradient exists in one dimension, such that the electron density increases with spatial direction x as shown in Figure 1.

As the electrons move through the semiconductor they are subject to many random collisions which change their direction of travel. This gives rise to the concept of a mean free path, or mean free time - the average distance or time an electron moves freely without collision. Assuming there is no electric field present, then the electrons can travel in any direction with equal probability in between collisions.

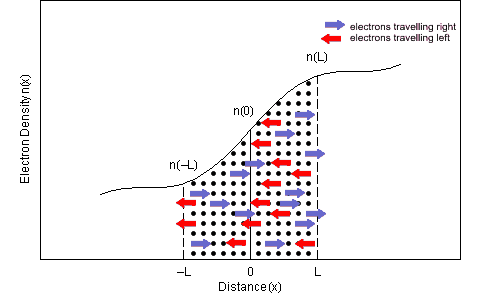
Figure 1. Electron concentration with distance. L is the mean free distance.

Consider what happens to the electron concentration gradient if electrons are allowed to disperse through the material through by random thermal motion. The regions –L and L are one mean free path distance away from the point x=0. We need to determine the net flux of electrons passing x=0. In the region from x=(-L, 0), half of the electrons will pass across the plane at x=0. Similarly, half of the electrons in the region from x=(0,L) will pass across the plane at x=0. If the concentration of electrons in each region were the same, then there would be no net flux of electrons across the plane. However, since the electron density in each region is different, there is a net flow of electrons across the plane at x=0.

In mathematical terms, the flux of electrons from in the region –L to 0 is

(1)

where v_th is the thermal velocity of the electrons while the number of electrons passing through the plane at x=0 from the region 0 to L is given by:

(2)

Hence the net flow of carriers from left to right is F₁-F₂.

(3)

Using a Taylor series expansion to approximate the densities at x=± L we obtain

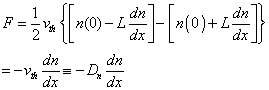
(4)

where D_n is known as the diffusivity. The current associated with diffusion is therefore,

(5)

Or in three dimensions,

(6)

It can be seen that the diffusion current is proportional to the rate of change of electron concentration. Electrons flow away from regions of high concentration to regions of low concentration until a equilibrium is reached. We shall see in the next section how the diffusivity and mobility are related through the Einstein relations.

Table 1. Electron and Hole Diffusivities of a few semiconductor materials.