|
|
The Equation of Continuity
The equation of continuity governs how injected carriers behave with time when they are injected into the semiconductor. It contains terms for the processes we have seen so far, such as generation, recombination, drift current and mobility. For simplicity we consider the flow of carriers in one-dimension.
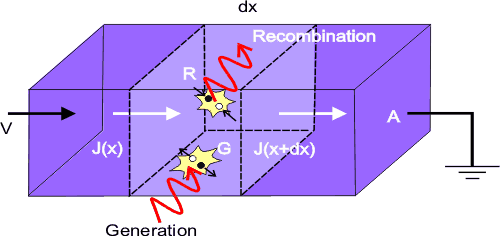
Figure 1. Conceptual view of the flow of electrons and holes to derive the equation of continuity.
Consider a block of semiconductor material of cross-sectional area A and an infinitesimal region within the semiconductor of thickness dx at x as shown Figure 1. With a potential difference V across the ends, the total number of electrons within this region at any time is the algebraic sum of the number of electrons flowing into the slice; the number of electrons flowing out of the slice; the number of electrons generated within the volume of the slice by and the number of electron-hole pairs removed by recombination within the volume of the slice. In mathematical terms,
![]()
(1)
Expanding the term for the current, Jn(x+dx) in terms of a Taylor series,
![]()
(2)
and substituting in (1) we obtain the equation of continuity for electrons.
![]()
(3)
A similar equation for holes can be derived with the only notable change being the negative sign for positive charge of the hole.
![]()
(4)
Where Rp is formed from nn-nn0/t n is the excess number of number of electrons in the excited state and t n is the recombination lifetime , typically of the order of a few picoseconds. The total current is given by the sum of the drift current and the diffusion current. For electrons:
![]()
(5a)
![]()
(5b)
Generation of electron-hole pairs is governed by the absorption process as left unchanged for the present moment. The final term is allows for recombination. The continuity equations
![]()
(6a)
![]()
(6b)
Valid for low current density in the classical Maxwell Boltzmann limit.
|
|