p-n Junctions and Heterostructures

Junctions are crucial to many semiconductor applications. The oldest method of making a p-n junction is by diffusion. The dopant diffuses in under heating so that the surface acceptor concentration exceeds the donor concentration. A junction appears when Nd=Na
A second technique is ion implantation. The starting material, n-type only, is bombarded with the required species of ions, say acceptors. This produces sharper junctions, but can cause damage to the crystal lattice structure increasing the number of dislocations and interstitial atoms.
A third technique is epitaxial deposition. The starting material is a single crystal in all cases, so it is possible to grow further crystal layers which are in register with the starting crystal; this is called epitaxy. The most precise although most expensive way of achieving this is Molecular Beam Epitaxy (MBE). Ion of the semiconductor together with dopants are fired at the crystal surface. Under the right conditions (ultra-high vacuum, correct ion fluxes, correct substrate temperature) the crystal grow epitaxially with the required dopant included. This technique can produce very sharp junctions and there is no counter-doping, i.e. no donors in the p-type region.
We now considers a p-n junction in the absence of voltage bias, so that it is in thermodynamic equilibrium. This means that the chemical potential ![]() must be constant across the junction. Since
must be constant across the junction. Since ![]() is near the valence band edge in a p-type region and near the conduction band in an n-type region, the bands must bend through the junction as shown below:
is near the valence band edge in a p-type region and near the conduction band in an n-type region, the bands must bend through the junction as shown below:
In the region where the bands are bending, ![]() is near the middle of the gap and therefore n<n0, p<p0, where n0 and p0 are the concentrations deep inside the n and p type regions. This is therefore called the depletion region. If we assume the junction is sharp, with Na and Nd changing abruptly at the junction, and if assume Nd=Na =, p0=Na, thus we see that within the depletion region p<Na on the left and n<Nd on the right. Since Na and Nd are the densities of ionised acceptor and donor ions, this means that there is a net negative charge on the p-type side of the junction, and a net positive charge on the n-type side. These separated charges generate an electric field, which is the physical cause of the band bending. The overall picture is summarised below.
is near the middle of the gap and therefore n<n0, p<p0, where n0 and p0 are the concentrations deep inside the n and p type regions. This is therefore called the depletion region. If we assume the junction is sharp, with Na and Nd changing abruptly at the junction, and if assume Nd=Na =, p0=Na, thus we see that within the depletion region p<Na on the left and n<Nd on the right. Since Na and Nd are the densities of ionised acceptor and donor ions, this means that there is a net negative charge on the p-type side of the junction, and a net positive charge on the n-type side. These separated charges generate an electric field, which is the physical cause of the band bending. The overall picture is summarised below.
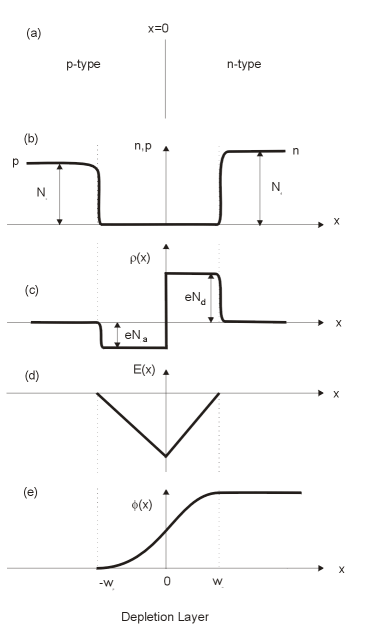
We now calculate charge, electric field and potential. First we find the band offset. ![]() , i.e. the difference in the height of
, i.e. the difference in the height of ![]() above the valence band on the two sides. In the n-type region, the value of
above the valence band on the two sides. In the n-type region, the value of ![]() relative to the local valence band is given by
relative to the local valence band is given by
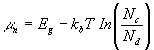 (2.1)
(2.1)
assuming Na=0 on the n-side. On the p-type side, we have
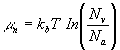 (2.2)
(2.2)
assuming Nd=0 on this side. These give
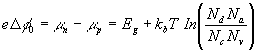 (2.3)
(2.3)
Using the definition of the intrinsic density ni (1.#), gives
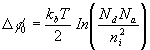 (2.4)
(2.4)
This is the difference in the electrostatic potential between the two sides since ![]() is the energy difference between electrons at the bottom of the conduction band on the two sides, as may be seen from the diagram.
is the energy difference between electrons at the bottom of the conduction band on the two sides, as may be seen from the diagram.
The variation of ![]() and the electric field
and the electric field ![]() across the junction can be calculated as long as the variations with x of Nd and Na are known. If we assume an abrupt junction then the charge distribution has the form
across the junction can be calculated as long as the variations with x of Nd and Na are known. If we assume an abrupt junction then the charge distribution has the form
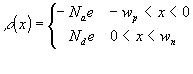 (2.5)
(2.5)
where wp and wn are the semi-widths of the depletion region on the p-side and n-side; values for them will be found later.
The electric field satisfies Gauss' law:
![]() (2.6)
(2.6)
since ![]() with
with ![]() constant, and in the present 1-d case
constant, and in the present 1-d case ![]() , this gives
, this gives
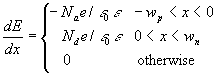 (2.7)
(2.7)
The boundary conditions are E=0 for x<-wp and x>wn since the junction is in equilibrium. The solution of (2.7) is therefore
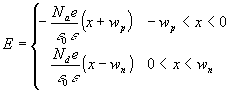 (2.8)
(2.8)
Furthermore, E must be continuous at x=0, which gives
![]() (2.9)
(2.9)
As seen from the figure, this is simply the condition of electrical neutrality of the whole depletion region. The variation of E with x given is shown in (d)
Equations (2.#) and (2.7) together give ![]()
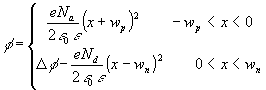 (2.10)
(2.10)
![]() must be continuous at x=0; this gives a second relation between wp and wn:
must be continuous at x=0; this gives a second relation between wp and wn:
![]() (2.11)
(2.11)
Recall that ![]() is already known from (28). The variation of
is already known from (28). The variation of ![]() with x given by (34) and (35) is shown in (c). As stated, (28), (33) and (35) can be solved for the values of wp and wn; they are
with x given by (34) and (35) is shown in (c). As stated, (28), (33) and (35) can be solved for the values of wp and wn; they are
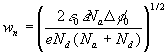 (2.12)
(2.12)
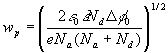 (2.14)
(2.14)
The dependence on T and on the doping deserves comment. Assuming for simplicity Na=Nd (equal doping on both sides) so that the factors.
The dependence on T and on the doping deserves comment. Assuming for simplicity Na=Nd (equal doping on both sides) so that the factors ![]() and
and ![]() are both one, substitution of (44) for
are both one, substitution of (44) for ![]() gives:
gives:
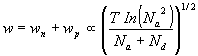 (2.15)
(2.15)
The logarithmic dependence is very weak compared with the denominator, so:
w increases as T increases
w decreases as doping Na+Nd increases
The application of p-n junctions depends on having an applied voltage so that a current flows through the junction. With a voltage V applied a difference eV appears between the values of ![]() on the p and n side. We distinguish between forward and reverse bias, as in the diagram below:
on the p and n side. We distinguish between forward and reverse bias, as in the diagram below:
The calculation of ![]() etc. go through much as before, and give:
etc. go through much as before, and give:
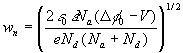 (2.16)
(2.16)
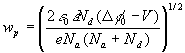 (2.17)
(2.17)
There is a charge separation in the depletion region. Thus the depletion region behaves like a capacitor, and the capacitance is given by
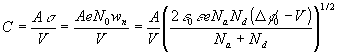 (2.18)
(2.18)
Where A is the area of the junction (in the y-z plane). This has the useful property that the capacitance can be varied by applied voltage. In practice, reverse bias is needed so that the current flow is small. A p-n junction device used as a voltage-variable capacitor is known as a varactor diode.
The important property of a p-n junction is the current-voltage characteristics. A derivation requires discussion of diffusion and recombination of carriers. The result is
![]() (2.19)
(2.19)
where the predominant temperature dependence of I0 is given by
![]() (2.20)
(2.20)
The first semiconductor lasers where made from heavily doped p-n junctions. Under conditions of forward bias the electrons and holes would recombine at the barrier junction producing some laser emission at high currents. These devices were inefficient and had high threshold currents as the majority carriers tended to drift away from the junction interface. It was soon discovered that more efficient lasers could be produced by the implementation of a heterostructure design.
Heterostructures
A heterostructure is a junction in a single crystal between two dissimilar semiconductors. It is convenient to use a notation where the narrow-bandgap semiconductor is denoted by lower case n or p and the wider band gap semiconductor with upper-case N or P according to its majority carriers. A Heterostructure can be isotype, in which case, both semiconductors have the same type of majority carriers. An anisotype heterojunction, has differing majority carriers in the semiconductor materials. By analysis of these two types of heterostructure we can consider the double heterostructure, a common feature in edge emitting semiconductor lasers.
In a heterostructure an alloy material is used such as Al in GaAs to change the band-gap of the material. In this material a small fraction of the Arsenic sites are occupied by Aluminium atoms.
Good quality heterostructures were not prepared before 1960 by Anderson. This discussion shall be restricted to properties of heterostructure relevant to laser design. Therefore only lattice matched heterostructures without interface states are considered here. One of the most important properties of heterojunctions is the carrier confinement provided by the wider energy gap semiconductor. The electron and hole confinement barriers and the leakage current due to unconfined carriers are considered.
GaAs-AlxGa(1-x)As Bandstructure
The major features of the energy band structure of GaAs are shown in the figure. The bandstructure depends on direction. The upper bands are the conduction bands while the lower bands are the valence bands. GaAs is a direct band semiconductor. The direct energy gap of high purity GaAs is 1.424eV at T=300K. Its variation with temperature can be expressed by:
![]() (2.21)
(2.21)
The energy gap shrinks for high carrier concentrations. The energy gap shrinkage is about 0.013eV for a hole concentration p=1x1018 cm-3
For computational purposes, it is convenient to express the energy gap as a function of composition. The ![]() direct energy gap may be represented by:
direct energy gap may be represented by:
![]() (2.22)
(2.22)
and
![]() (2.23)
(2.23)
The electron effective mass for the ![]() conduction band is given by
conduction band is given by
![]() (2.24)
(2.24)
and the density of states hole mass for AlxGa(1-x)As is taken as
![]() (2.25)
(2.25)
Heterojunction Energy Band Diagrams
Heterojunction energy band diagrams are obtained by assuming that the bulk properties are retained up to the heterojunction interface. The energy band profile is shown for p-GaAs and N- AlxGa(1-x)As. The space charge regions are neglected so that the energy band profiles can be taken as constant with distance. The subscripts refer to the GaAs and AlxGa(1-x)As respectively. The conduction and valence bands are represented by Ec and Ev, the Fermi levels by F, and the difference between the edge and the Fermi level is ![]() .
.
The position of the conduction band with respect to the vacuum level is assumed to be given by the electron affinity ![]() . Electron affinity is defined as the energy necessary to take an electron from the conduction band to the vacuum level. The work function
. Electron affinity is defined as the energy necessary to take an electron from the conduction band to the vacuum level. The work function ![]() is the energy required to take an electron from the Fermi level to the vacuum level. Since the work function depends on the Fermi level, which varies with impurity concentration it is more convenient to use the electron affinity. Electron affinity is very difficult to determine and is generally assigned from capacitance measurements by interpretation based on this model of photoelectric emission measurements.
is the energy required to take an electron from the Fermi level to the vacuum level. Since the work function depends on the Fermi level, which varies with impurity concentration it is more convenient to use the electron affinity. Electron affinity is very difficult to determine and is generally assigned from capacitance measurements by interpretation based on this model of photoelectric emission measurements.
From the figure, it is apparent that the discontinuity in the conduction band is the difference in the electron affinities.
![]() (2.26)
(2.26)
and
![]() (2.27)
(2.27)
The last equation, rearranged gives the discontinuity in the valence bands as
![]() (2.28)
(2.28)
and emphasises that
![]() (2.29)
(2.29)
This is an important result because ![]() and
and ![]() are accurately known for AlxGa(1-x)As, while the differences in electron affinities is not.
are accurately known for AlxGa(1-x)As, while the differences in electron affinities is not.
Fermi Level Determination
At thermal equilibrium the Fermi level must be constant throughout the heterojunction. Therefore, in the same manner as for the p-n junction, the band-bending at the heterojunction interface is given by the difference in Fermi levels on the p- and N-sides. This difference in Fermi levels is the built in potential Vd and is given by
![]() (2.30)
(2.30)
This equation also applies to other anisotype (different semiconductor materials) and isotype heterojunctions. The Fermi level is determined by the condition of electrical neutrality:
![]() (2.31)
(2.31)
The other condition that must be satisfied is
![]() (2.32)
(2.32)
where ni is the intrinsic carrier density and the ![]() 's are the activity coefficients. In the cases considered here they will be taken as unity. The electron and hole concentrations are
's are the activity coefficients. In the cases considered here they will be taken as unity. The electron and hole concentrations are
![]() (2.33)
(2.33)
and
![]() (2.34)
(2.34)
where ![]() and
and ![]() where given by
where given by
![]() (2.35)
(2.35)
and
![]() (2.36)
(2.36)
For localised impurities, the probability P(E) an electron of either spin occupying the level is given by
![]() (2.37)
(2.37)
The factor of 1/2 is generally called spin degeneracy factor. If there are Nd donors, the number of neutral donors (donors with electrons) is given by
![]() (2.38)
(2.38)
Where Ed is the donor level. The number of ionised donors Nd+ is simply Nd
- Nd0, which gives
![]() (2.39)
(2.39)
Similarly for acceptors
![]() (2.40)
(2.40)
![]() (2.41)
(2.41)
where Ea is the acceptor level. It is convenient to assign Ev as E=0 so these quantities are related to their position relative to the valence band.
It has been customary to give the acceptor ionisation energy as Ea-Ev, which is also the acceptor level and to give the donor ionisation energy as Ec-Ed.
Electrical measurements of AlxGa(1-x)As doped with Sn and AlxGa(1-x)As doped with Ge and Te showed that Ea-Ev and Ec-Ed increase with x.
We need to evaluate the spatial variation of the built-in potential on each side of the heterojunction interface. When two semiconductors are brought into contact, the Fermi level must be constant throughout the solid at thermal equilibrium.
The Fermi level is the chemical potential or free energy of the electrons and holes. The diagram is draw as below:
Because the majority carrier hole density on the p-side is much greater than the minority carrier hole concentration on the N-side, there then will be a hole diffusion current due to this large concentration gradient. The one-dimensional diffusive hole current density per unit area is given by
![]() (2.42)
(2.42)
where Dp is hole diffusivity. The diffusivity is related to the mobilty by Einstein relation
![]() (2.43)
(2.43)
where ![]() is the hole mobility. The diffusive electron current is
is the hole mobility. The diffusive electron current is
![]() (2.44)
(2.44)
where Dn is the electron diffusivity. The holes on the p-side and electrons on the N-side diffuse across the junction and recombine, which leaves behind regions containing the charged immobile acceptors and donors as shown.
These depleted regions near the heterojunction interface constitute the space-charge region. The space charge results in a built-in field that opposes the carrier diffusion. The heterojunction interface region is depleted of majority carriers until the drift current due to the built in field E is sufficient to exactly balance the diffusion current.
At thermal equilibrium, the total hole and electron currents must be zero. The total electron current density is
![]() (2.45)
(2.45)
A similar expression results for holes. When the electron concentration can be represented by the exponential form the (85) becomes:
![]() (2.46)
(2.46)
with ![]() . This last equation shows that the slope of the conduction band with distance is qE. Flat band edges mean that E=0 and the in the space-charge region
. This last equation shows that the slope of the conduction band with distance is qE. Flat band edges mean that E=0 and the in the space-charge region ![]() , so that the energy band diagram must be modified to account for the built in field. The details of the built in field can be found most redily from Poisson's equation. In one-dimension,
, so that the energy band diagram must be modified to account for the built in field. The details of the built in field can be found most redily from Poisson's equation. In one-dimension,
![]() using the relation
using the relation ![]() .For a static field, the potential V is related to the field by
.For a static field, the potential V is related to the field by
![]() ,(2.47)
,(2.47)
and so Maxwell's equation can be written,
![]() (2.48)
(2.48)
which is Poisson's equation. The charge density is the sum of all the charged species:
![]() (2.49)
(2.49)
The solution is obtained by assuming that the mobile carrier concentrations can be neglected in the space-charge region. The potential on the p-side is taken as Vp and the potential on the N-side is taken as VN. The edges of the space charge region are taken as xp and xN. Poisson's equation may then be written:
![]() (2.50)
(2.50)
![]() (2.51)
(2.51)
and
![]() (2.52)
(2.52)
For GaAs=e 1=13.1e 0 and e for AlAs is 10.06e 0 .By using linear interpolation, e 2 for AlxGa(1-x)As is given by
e AlxGa(1-x)As =e 2=(13.1-3.0x) e 0
Double Heterojunctions
Two Heterojunctions placed end to end can form a double heterostructure. For example, a PnN double heterostructure can be thought of as a Pn heterostructure and a nN heterostructure sharing the same small band gap semiconductor region.
Quantum Well
When the smaller band gap region width becomes of the order of a few nanometres, the electrons become confined in one of the three dimensions. This confinement causes discrete energy levels to become more apparent. The quantum well forms a well defined region were recombination can occur. This an important feature in low threshold current semiconductor laser devices.
Density of States
The density of states is a measure of how many electron states can occupy an energy range from E to E+dE per unit volume. It is not possible to determine the exact position and momentum of an electron simultaneously. Constraining the position x leads to greater uncertainty in the momentum p and vice-versa. The property is expressed in the Heisenburg uncertainty principle.
![]() (2.53)
(2.53)
Consider an electron constrained to move in one-dimension along a line of length ![]() . There is uncertainty in its position. From the Heisenburg uncertainty principle, the uncertainty in its velocity is
. There is uncertainty in its position. From the Heisenburg uncertainty principle, the uncertainty in its velocity is
![]() (2.54)
(2.54)
If we consider only a certain velocity range between v1 and v2, the number of separately distinguishable velocities will be
![]() (2.55)
(2.55)
If we now allow the electron to move in three dimensional cube of side ![]() . Instead of merely along a line, all possible velocities must lie in a spherical shell of inner radius v1 and outer radius v2. The volume of the shell in velocity space is
. Instead of merely along a line, all possible velocities must lie in a spherical shell of inner radius v1 and outer radius v2. The volume of the shell in velocity space is
![]() (2.56)
(2.56)
Each velocity is separated by ![]() , therefore a unit volume of velocity space occupies
, therefore a unit volume of velocity space occupies ![]() . The number of allowed velocities v1 and v2 is given by:
. The number of allowed velocities v1 and v2 is given by:
![]() (2.57)
(2.57)
![]() (2.58)
(2.58)
![]() (2.59)
(2.59)
Finally, by the Pauli exclusion principle, two electrons can occupy each state. For a cube of unit length the density of states per unit volume is given by:
![]() (2.60)
(2.60)
The kinetic energies associated with each velocity are
![]() (2.61)
(2.61)
![]() (2.62)
(2.62)
gives
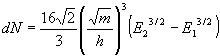 (2.63)
(2.63)
If we allow E1 to approach E2 so that
![]()
![]()
we obtain
![]() (2.66)
(2.66)
This value of dN is the number of electrons, having energies lying between E and E+dE, which can be accommodated in unit volume of a semiconductor crystal.
The density of single states per unit energy for the conduction band is given by
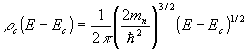 (2.67)
(2.67)
Similarly for the valence band
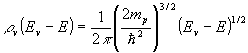 (2.68)
(2.68)