Distribution Functions
How a system of particles can be distributed, depends very much on the properties of those particles. Classically, particles are distinguishable from one another. In this situation, the Boltzmann distribution function is the distribution function of choice. When particles are indistinguishable from one another there are fewer ways of arranging them. However, there is a further consideration, this is the spin of the particle. Sub-atomic particles have a property of spin which is a measure of their angular momentum. The particles can be classified into those Particles that have integral spin. i.e. h,2h,3h etc. Such particles are known as Bosons and include photons, phonons and composite particles comprising of an even number of member particles.
Another classification of particles have half-integral spin. i.e. h/2,2h/3, 3h/5, etc and are known a Fermions. The class of Fermions includes electrons, protons, muons, pions, etc.
Fermions and Bosons occupy energy levels in different ways. Fermions, which include electrons in the same state are forbidden from occupying the same energy levels. However, electrons in the same state can have spin +1/2 or -1/2 therefore only two electrons may occupy a given energy level.
Bosons have different rules. Any number of Bosons may occupy the same quantum state. We use a number of distribution functions to deal with the probability of a particle occupying a particular energy level. These are:
![]() (Boltzmann distribution)
(Boltzmann distribution)
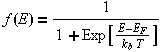 (Fermi-Dirac distribution)
(Fermi-Dirac distribution)
![]() (Bose-Einstein distribution)
(Bose-Einstein distribution)
Where EF is the chemical potential or Fermi energy. This is the energy at which there is a 50% probability of the electron being in the conduction band or valence band. See also approximations for the Fermi Level. Therefore they are a measure of the probability of an energy state being occupied by a particle. The probability of an energy level being occupied is dependent on the temperature and the Fermi energy.
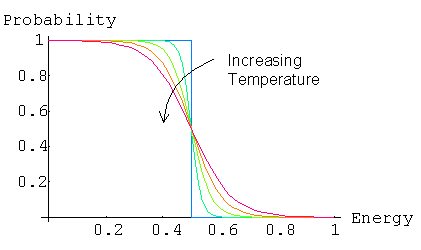
At absolute zero, in a intrinsic semiconductor, all of the energy levels within the valence band are occupied. There is a 100% chance of an electron being in an energy level in the valence band and 0% of an electron occupying a state in the conduction band. The Fermi level is the last filled energy level in the valence band.
As the temperature increases electrons from the valence band have small probability of gaining enough thermal energy to enter the conduction band. The greater the temperature the more chance that an electron has of occupying an energy level in the conduction band.
When the Fermi distribution is multiplied by the density of states, and integrated over the energy of the band the carrier concentration is results.
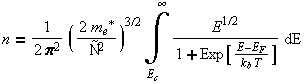
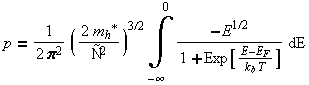
However, often in the modeling of these processes, we know the carrier concentration but we need to find the Fermi energy. This is a more difficult problem with no analytical solution. However a number of approximation techniques have been developed to calculate the Fermi energy.